幾何学
2022年01月23日
続 先輪はなぜ小さいのか
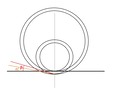 この図を示せば、何も説明は要らないだろう。α<βであるから、小さな先輪のフランジ先端がレイル面に当たる位置は、大きな動輪のフランジが当たる位置より、ずっと手前にある。すなわち脱線しにくい。
この図を示せば、何も説明は要らないだろう。α<βであるから、小さな先輪のフランジ先端がレイル面に当たる位置は、大きな動輪のフランジが当たる位置より、ずっと手前にある。すなわち脱線しにくい。もちろん、フランジ形状、摩擦係数などのファクタはあるが、脱線しにくいのは小径車輪であることは間違いない。気になる方は、レイル面でフランジを切った断面図を描かれると良いだろう。それが曲線上でどうなるかである。
それでもわからない方は、ふすまのはまっている敷居の溝の中を考えると良いだろう。ビー玉を転がすのと、大きなボウリングのボールを転がすのとでは、どちらが外れにくいかである。当然ビー玉の方が外れにくい。
このようなわけで、小さな軸重が掛かっているだけで、復元力を大きくしても外れない。だから誘導輪としての効果を発揮する。模型の場合も同様の筈だが、HO以下では、復元力はほとんど無きが如しである。復元力が無いと、かえって脱線しやすいようにも思うが、それについて研究された方は居るのだろうか。
先回お見せしたUP835は先従輪の復元力が極めて大きいので、動輪のフランジはほとんど触らないはずだ。ある人はフランジレス動輪でも走るのではないかと言ったほどだ。
ボールベアリングの外輪をローラとして、V字斜面の中心に転がり落ちるようになっている。先輪は摩擦の少ないステンレス製 Low-D であるから、脱線の可能性は極めて小さい。
2020年07月22日
unversal joint の角速度変化
northerns484氏のブログで展開されているユニヴァーサル・ジョイントの角速度の変化が興味深い。
どういうわけか、模型界ではこの部分の間違いが多い。数で言えばラジコンの方がずっと多いだろう。市販されているパーツはほとんどが間違っている。これは数年前の調査結果だが、今もさほど変化していないと思う。
ラジコンではタイヤがスリップしているのが普通で、めちゃくちゃなドリフトをさせるのが目的だから、等速であることにそれほどの価値があるとも思えないのだろう。 だから、分かっている人も声を出さないのではないかと推測している。
翻って鉄道模型ではどうだろう。高価なブラス製の機関車、電車がゴリゴリと音を立てながら走ったら、腹が立つはずだ。模型製作工場では急曲線を通さないのだろう。直線を往復させて合格ということにしているのではないか。
今回、部材の長さを測定した結果から計算した結果が発表されている。角速度の変化はかなりある。我慢できる状態とそうでない状態の境目がはっきりしたように思う。
模型メーカはその後改善されたのだろうか。店頭にある部品を回収するか、どうすれば改善されるかを説明する紙を添えるべきであるが、それはなされているのだろうか。
どういうわけか、模型界ではこの部分の間違いが多い。数で言えばラジコンの方がずっと多いだろう。市販されているパーツはほとんどが間違っている。これは数年前の調査結果だが、今もさほど変化していないと思う。
ラジコンではタイヤがスリップしているのが普通で、めちゃくちゃなドリフトをさせるのが目的だから、等速であることにそれほどの価値があるとも思えないのだろう。 だから、分かっている人も声を出さないのではないかと推測している。
翻って鉄道模型ではどうだろう。高価なブラス製の機関車、電車がゴリゴリと音を立てながら走ったら、腹が立つはずだ。模型製作工場では急曲線を通さないのだろう。直線を往復させて合格ということにしているのではないか。
今回、部材の長さを測定した結果から計算した結果が発表されている。角速度の変化はかなりある。我慢できる状態とそうでない状態の境目がはっきりしたように思う。
模型メーカはその後改善されたのだろうか。店頭にある部品を回収するか、どうすれば改善されるかを説明する紙を添えるべきであるが、それはなされているのだろうか。
2016年03月29日
続々 wye (Y) switch
 #8ポイントの簡易キットがいくつあるか調べた。左右3本ずつだと思っていたが、右がもう1本見つかった。これで機廻り線の分岐ができる。とは言っても、行き止まり部分にもう1本は必要だから、それは作らねばならない。
#8ポイントの簡易キットがいくつあるか調べた。左右3本ずつだと思っていたが、右がもう1本見つかった。これで機廻り線の分岐ができる。とは言っても、行き止まり部分にもう1本は必要だから、それは作らねばならない。机の上を整理して並べてみた。複線間隔を所定の値にするときのフログ間距離を求めねばならない。計算値と、並べたときの実測距離が一致したので、一安心だ。このキットはレイルをかなり短く切っているので、必要なフログ間距離を得るには、ある程度の長さのレイルを足さねばならない。
材料箱を探すと、短いレイルを捨てずに取ってあった。ちょうど良いものがたくさんあり、2,3 mm切るだけでぴったりであった。
これで第三期工事の準備は終わりである。
 客車ヤード(第二期工事)を先にせねばならない。この部分はかなり面倒である。分岐が曲線部に集中し、すべて曲線ポイントになる。すなわち番手が大きくなる。#10のポイントを曲げて作り直せば、そこそこのものができる。4本あるので5線のヤードができることになる。すべて現物合わせで作り直す。一応並べてみて、大体の構成を頭に入れたが、その通りにはできないかもしれない。フログも曲げることになるが、それは可能である。
客車ヤード(第二期工事)を先にせねばならない。この部分はかなり面倒である。分岐が曲線部に集中し、すべて曲線ポイントになる。すなわち番手が大きくなる。#10のポイントを曲げて作り直せば、そこそこのものができる。4本あるので5線のヤードができることになる。すべて現物合わせで作り直す。一応並べてみて、大体の構成を頭に入れたが、その通りにはできないかもしれない。フログも曲げることになるが、それは可能である。曲線部は複線間隔を狭くできない。しかも長い客車であるから、本線と同じにする。この部分の分岐の配置はかなり雑然とした感じになるが、なるべくS字カーヴを避けた機能第一の設計になる。客は乗っていないのだから、それでよい筈だ。実物のヤードも継ぎ足したり、障害物を避けて極端な曲線になっていることがある。
この写真の曲線の線路は、隠しヤードへの線路である。その右の5線は客車ヤードの線路位置を示している。直線部分はこれだけで、あとは曲線である。 観客からは見えにくい位置なので、線路の素性は様々である。
2015年01月29日
続々 勾配区間の建設
 骨組みの上に板を載せてみた。ネジで仮留めしてある。台形の板を 24 mm の構造用合板から切り出した。板が、出たり入ったりしているのは耳が切り落としてないからだ。全体を固定してから、コンパスで卦書いて切り落とす。
骨組みの上に板を載せてみた。ネジで仮留めしてある。台形の板を 24 mm の構造用合板から切り出した。板が、出たり入ったりしているのは耳が切り落としてないからだ。全体を固定してから、コンパスで卦書いて切り落とす。勾配を測定すると、当然のことながら、一定にはならない。
その様子を見て、昔、韓国製の鉄道模型が現れた頃のことを思い出した。筆者はそのウォームギヤを見て、とても驚いた。斜面が一定でないのだ。一周が20くらいの面で出来ていたのだ。おそらくホブと云う刃物で切っているのだが、回転数が低いのか、何なのか分からないが、螺旋の斜面が多面体なのである。廻すと当然、ゴロゴロ言う。そういう製品があったのだが、最近はその種の問題は解決している。
しかし他の面では問題はまだ多い。
さて、用意してあるシムを挟んでみて様子を見た。計算値のシムを挟むと、かなり緩和される。お世話になった数学の専門家には感謝する。2800Rと2900Rの線路を載せてみると、斜面が一定であることが分かる。
コメントを戴いたが、蒸気機関車単機で100輌のブラス製貨車編成を牽くというのが、この博物館の「売り」である。おそらくこれをO scaleで実現できるところは、世界中探してもここしかないはずである。以前ミシガン州で廃業したスーパーマーケットでは200輌運転をするのを見たが、それはプラスティック製貨車を多重連のディーゼルで牽いていた。
Big Boyでなくても牽くことは可能だ。以前の実験ではSP5000でも可能であった。
2015年01月27日
続 勾配区間の建設
 角スタッドを切って、支柱に取り付けたところである。インパクト・レンチを用いて、鉄骨にドリルネジをねじ込む。こうして見ると、螺旋を直線で近似するのは無理であると云う事を実感する。柱間隔をもっと細かくすれば良いのだろうが、費用が掛かりすぎる。このようにある程度区間を分けておいて、シムをはさんで近似するというのが現実的であろう。シムの厚みは最大2mmほどである。
角スタッドを切って、支柱に取り付けたところである。インパクト・レンチを用いて、鉄骨にドリルネジをねじ込む。こうして見ると、螺旋を直線で近似するのは無理であると云う事を実感する。柱間隔をもっと細かくすれば良いのだろうが、費用が掛かりすぎる。このようにある程度区間を分けておいて、シムをはさんで近似するというのが現実的であろう。シムの厚みは最大2mmほどである。十分な量の24mmの合板を安く買ってある。それを一区間ごとに台形に切って、置いてみれば、どうすべきかはすぐわかる。当初は薄い12mmの合板を使う予定であったが、シムを連続的に貼らねば凹凸が表に出てしまうことが分かり、それは取りやめた(この状態を、現場の人たちの間では、「痩せ馬の骨が出る」という表現をするらしい)。
水準器を置いて、どの区間も水平が出ていることは確かめてある。たったの半周強ではあるが、この高低差を稼ぎ出す勾配区間の設計には大変な労力を必要とした。
板を載せてみると、複々線のホースシュウ・カーヴの様子がよくわかる。完成時に目を低くして透かして見ても不自然でないようなレベルにはできているはずだ。
4本の線路はそれぞれがカントを持ち、同じように傾いて走る。ここを100輌編成の列車が登り下りするのである。その様子を思い浮かべて、幸福な気持ちになる。
2015年01月25日
勾配区間の建設
平面部分の骨組みはかなり前に完成しているのだが、勾配区間は計算が面倒で、遅れ気味であった。平面の板をつなぎ合わせても、滑らかな螺旋にはならない。当初は支柱間隔を広くしていたのだが、補正量が大きく、とても無理だと分かった。仕方なく、1450mm間隔に支柱を立てることにした。こうすれば、調整用シムの厚さが薄くなる。
設計では垂直荷重だけ受け持たせることにして、水平方向の力は曲線の両端で受けていた。ところが角が多くなったので、各支柱に水平方向の動きに耐える構造を持たせねばならなくなった。足を十文字にすれば良いのだが、足が平面になるようにするのは素人の熔接では無理だ。
 カブースの煙突などには、このような倒れ止めがついている場合がある。一本の支えを付けるだけで、かなりの力に耐える。4 mm厚のフラットバーを床に留め、四角柱の垂直を見ながら、熔接すれば良い。これは工作が簡単である。この程度の厚さで、押し引きどちらにも十分耐える。
カブースの煙突などには、このような倒れ止めがついている場合がある。一本の支えを付けるだけで、かなりの力に耐える。4 mm厚のフラットバーを床に留め、四角柱の垂直を見ながら、熔接すれば良い。これは工作が簡単である。この程度の厚さで、押し引きどちらにも十分耐える。
 カーペットを敷いた後での熔接であるから、完全な養生が必要である。クラブの会員の足立健一氏が耐火性の布で養生シートを作ってくださったので助かる。氏はF1レースなどの耐火服を作る専門家である。熔鉱炉の横で仕事をする人たちの耐火服など、特殊な服を作っている。
カーペットを敷いた後での熔接であるから、完全な養生が必要である。クラブの会員の足立健一氏が耐火性の布で養生シートを作ってくださったので助かる。氏はF1レースなどの耐火服を作る専門家である。熔鉱炉の横で仕事をする人たちの耐火服など、特殊な服を作っている。
このような柱の根元を巻いて、さっと置けるように、切れ目を入れて下さった。三層構造で、中には耐火フェルトが挟んであり、熱が伝わりにくい。焼けたアイロンを置いたままにしても火事にならないそうである。オレンジ色の布は、最近の消防士の服装で見かけた方もあるだろう。燃えない布である。
 床を完全に保護した後で、周りに飛ぶといけないから、合板で囲いをつくる。そして、先日紹介した火花除けシートをかぶせる。熔接部分から10 cm程度離しておくことを忘れてはいけない。これで手前の隙間から熔接棒を差し込んで出来上がりである。面白いことに、熔接時に出る煙(フューム)は大半がシートにくっつくように感じる。作業終了後、シートを洗うと、白っぽい粉が落ちる。
床を完全に保護した後で、周りに飛ぶといけないから、合板で囲いをつくる。そして、先日紹介した火花除けシートをかぶせる。熔接部分から10 cm程度離しておくことを忘れてはいけない。これで手前の隙間から熔接棒を差し込んで出来上がりである。面白いことに、熔接時に出る煙(フューム)は大半がシートにくっつくように感じる。作業終了後、シートを洗うと、白っぽい粉が落ちる。
設計では垂直荷重だけ受け持たせることにして、水平方向の力は曲線の両端で受けていた。ところが角が多くなったので、各支柱に水平方向の動きに耐える構造を持たせねばならなくなった。足を十文字にすれば良いのだが、足が平面になるようにするのは素人の熔接では無理だ。
 カブースの煙突などには、このような倒れ止めがついている場合がある。一本の支えを付けるだけで、かなりの力に耐える。4 mm厚のフラットバーを床に留め、四角柱の垂直を見ながら、熔接すれば良い。これは工作が簡単である。この程度の厚さで、押し引きどちらにも十分耐える。
カブースの煙突などには、このような倒れ止めがついている場合がある。一本の支えを付けるだけで、かなりの力に耐える。4 mm厚のフラットバーを床に留め、四角柱の垂直を見ながら、熔接すれば良い。これは工作が簡単である。この程度の厚さで、押し引きどちらにも十分耐える。 カーペットを敷いた後での熔接であるから、完全な養生が必要である。クラブの会員の足立健一氏が耐火性の布で養生シートを作ってくださったので助かる。氏はF1レースなどの耐火服を作る専門家である。熔鉱炉の横で仕事をする人たちの耐火服など、特殊な服を作っている。
カーペットを敷いた後での熔接であるから、完全な養生が必要である。クラブの会員の足立健一氏が耐火性の布で養生シートを作ってくださったので助かる。氏はF1レースなどの耐火服を作る専門家である。熔鉱炉の横で仕事をする人たちの耐火服など、特殊な服を作っている。このような柱の根元を巻いて、さっと置けるように、切れ目を入れて下さった。三層構造で、中には耐火フェルトが挟んであり、熱が伝わりにくい。焼けたアイロンを置いたままにしても火事にならないそうである。オレンジ色の布は、最近の消防士の服装で見かけた方もあるだろう。燃えない布である。
 床を完全に保護した後で、周りに飛ぶといけないから、合板で囲いをつくる。そして、先日紹介した火花除けシートをかぶせる。熔接部分から10 cm程度離しておくことを忘れてはいけない。これで手前の隙間から熔接棒を差し込んで出来上がりである。面白いことに、熔接時に出る煙(フューム)は大半がシートにくっつくように感じる。作業終了後、シートを洗うと、白っぽい粉が落ちる。
床を完全に保護した後で、周りに飛ぶといけないから、合板で囲いをつくる。そして、先日紹介した火花除けシートをかぶせる。熔接部分から10 cm程度離しておくことを忘れてはいけない。これで手前の隙間から熔接棒を差し込んで出来上がりである。面白いことに、熔接時に出る煙(フューム)は大半がシートにくっつくように感じる。作業終了後、シートを洗うと、白っぽい粉が落ちる。2014年12月03日
複々線の路盤設計
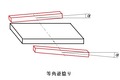
 複線の本線が、ホースシュウ・カーヴを描く場所がある。往きと還りで複々線になる。そのうちの2800R、2900Rの路盤付き線路はすでにあるのだが、3000Rと3100Rを作らねばならない。小さい二つの半径の路盤は写真のように重ねられる(stackable)設計で、可搬式組立て式レイアウトであった。それを半固定式にしてしまうので、隣に来る路盤はこの線路と同様なカントを持たねばならない。カントの勾配は3%ほどだ。
複線の本線が、ホースシュウ・カーヴを描く場所がある。往きと還りで複々線になる。そのうちの2800R、2900Rの路盤付き線路はすでにあるのだが、3000Rと3100Rを作らねばならない。小さい二つの半径の路盤は写真のように重ねられる(stackable)設計で、可搬式組立て式レイアウトであった。それを半固定式にしてしまうので、隣に来る路盤はこの線路と同様なカントを持たねばならない。カントの勾配は3%ほどだ。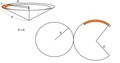 製作を簡略化するためには路盤自身を傾けてやれば良いのだが、その路盤の展開図の半径は線路半径より微妙に大きくなる。非常に浅い円錐面になるが、作図して計算すると、3000Rであれば1mm強大きくすればよいことが分かった。路盤幅も微妙に広くなる。それで決まりかと思っていたが、数学の専門家に会った時に、線路図を見せたところ、「勾配が付いているのを忘れているのではないか?」という指摘を受けた。
製作を簡略化するためには路盤自身を傾けてやれば良いのだが、その路盤の展開図の半径は線路半径より微妙に大きくなる。非常に浅い円錐面になるが、作図して計算すると、3000Rであれば1mm強大きくすればよいことが分かった。路盤幅も微妙に広くなる。それで決まりかと思っていたが、数学の専門家に会った時に、線路図を見せたところ、「勾配が付いているのを忘れているのではないか?」という指摘を受けた。「螺旋の一部であるから、平らにすると多少半径が大きくなるよ。」と言う。
「これは普通の幾何学では計算できないけど、僕の専門分野だから計算してあげよう。」と言ってくれた。3日後に、数値を入れた結果を戴いた。空間曲線曲率という概念だそうだ。見たことが無い数学記号がたくさんあった。螺旋に内接する円をたくさん描いて近似する方法である。詳しく説明してくれたのだが、ほとんど理解できなかった。
1.5%の勾配だと、3000.000Rが3000.675Rになるそうだ。カントによる効果の方がずっと大きい。施工の時の誤差の方が、さらに大きいから、こちらの方は無視できるだろう。
この数値を入れた図面を作り、NCフライス工場に頼めば一応は準備完了だ。
2014年02月05日
sine と tangent
先日のコメントでサインとタンジェントの話が出た。いつも、どちらで書こうか迷って、結局タンジェントにする。模型ではタンジェントの方が分かりやすいし実用的である。水平な路盤に印を付けて、持ち上がる量を決めるからだ。

実物はサインでないと定義しにくい。線路は山中の斜面に敷くので、走行距離当たりの持ち上がり量を考えねばならない。地中に仮想の線を引くわけにもいかないからだ。
機関車の走行距離と負荷を持ち上げる高さで角度が定義され、走行速度が分かれば出力が算出される。これは機関車の効率を測る方法である。
機関車は斜面を登るわけだから、サインなのだが、鉄道の勾配は非常に緩やかなので、実質的にはサインとタンジェントの値は等しいと近似しても、なんら問題はない。
Incline (いわゆるケーブルカー)などではその差は如実に表れる。
コメントにも書いたが、この実験のように路盤にShim(薄い板)を挟んで持ち上げるときは、タンジェントの方が楽である。床のタイルの大きさの整数倍のところに薄い板をはさんで測定し、そのシムの厚さをノギスで測定すれば済むからだ。これをサインでやれということになると、路盤長さを測定して印を入れ、そこにシムをきちんと挟まねばならない。かなり面倒だ。
というわけで、「本当はサインを用いるが、鉄道模型ではタンジェントが楽。」が正解ということを強調しておく。

実物はサインでないと定義しにくい。線路は山中の斜面に敷くので、走行距離当たりの持ち上がり量を考えねばならない。地中に仮想の線を引くわけにもいかないからだ。
機関車の走行距離と負荷を持ち上げる高さで角度が定義され、走行速度が分かれば出力が算出される。これは機関車の効率を測る方法である。
機関車は斜面を登るわけだから、サインなのだが、鉄道の勾配は非常に緩やかなので、実質的にはサインとタンジェントの値は等しいと近似しても、なんら問題はない。
Incline (いわゆるケーブルカー)などではその差は如実に表れる。
コメントにも書いたが、この実験のように路盤にShim(薄い板)を挟んで持ち上げるときは、タンジェントの方が楽である。床のタイルの大きさの整数倍のところに薄い板をはさんで測定し、そのシムの厚さをノギスで測定すれば済むからだ。これをサインでやれということになると、路盤長さを測定して印を入れ、そこにシムをきちんと挟まねばならない。かなり面倒だ。
というわけで、「本当はサインを用いるが、鉄道模型ではタンジェントが楽。」が正解ということを強調しておく。
2013年08月30日
「等角逆捻り機構の工夫」
 トークショウに引き続いて、今野氏の旋盤を用いた動輪の作成の実演があった。小型旋盤を現場まで送って、それをセッティングするので、大変なご苦労だ。位置決めピンが一本飛んでしまったそうで、QCTPがクウィック・チェンジでなくなってしまうという障碍が起き、それを乗り越えての講演で、さぞかし大変であったろう。筆者だったら、止めてしまいそうな状況だった。紹介記事があるので、それを参照されたい。
トークショウに引き続いて、今野氏の旋盤を用いた動輪の作成の実演があった。小型旋盤を現場まで送って、それをセッティングするので、大変なご苦労だ。位置決めピンが一本飛んでしまったそうで、QCTPがクウィック・チェンジでなくなってしまうという障碍が起き、それを乗り越えての講演で、さぞかし大変であったろう。筆者だったら、止めてしまいそうな状況だった。紹介記事があるので、それを参照されたい。今野さん、本当にお疲れ様。
そのあと、筆者の等角逆捻り機構の講演だ。何人かの方から、「タイトルの意味が分かりにくい。」とお叱りを受けていた。現にグーグルでこの言葉を検索されて、当ブログに来訪された方が数十人いらっしゃる。それらの方は、「予習」を済まされてのご参加であるから、さほどの困難は無かったものと推察する。問題は、「何だろう」と思っていらした方たちだ。きっとよく分からないままではなかったか、と冷や汗が出た。
このようなメカニズム主体の分野は、ご自分でブラス板を切って穴空け、ヤスリがけ、ハンダ付けをしたことがない人には分かりにくいかもしれない。
出席者は少なくて5人、多くても30人と踏んでいたのであるが、100人弱ほどいらして、後の方の方は見えなかったのではないかと、申し訳ない気持ちで一杯である。
今回は、
1 三点支持の性能が、前後進で異なること。
2 ロンビック・イコライザが、非常に特殊な場合にのみ成り立つ「特殊解」であること。
3 ロンビック・イコライザの効果を得るには、他にも無数の解があること。
4 フカひれイコライザ ≠ ロンビック・イコライザであること。
5 ロンビック、フカひれは、等角逆捻り機構という概念に統一されること。
6 等角逆捻り機構は伊藤剛氏の命名で、根本的には二点支持であること。
7 「制御された二点支持」という概念を理解すると、様々な応用例があること。
8 いかなる線路にも追随するような懸架装置を採用することによって生じる利点。
についてお話しした。
作例も3種用意して行った。それと二軸台車のボルスタが倒れないようにした事例も用意した。これは現場で箱を開いて見たら、ネジが抜け落ちていた。それを嵌めるのに大わらわで、結局のところ、講演中に浮津信一朗氏のお手を煩わせて、締めて戴いた。この場を借りて御礼申し上げる。今野氏のお手製のロンビック・イコライザの見本をお借りしていたので、それもお見せした。
2013年03月16日
続 さらに等角逆捻り機構
Chicagoに来ている。今回は、レンタカーを借りなかった。空港から鉄道だけを使ってホテル近辺まで行けると書いてあったのでそれを試したのだ。近くの駅まではホテルの車に迎えに来てもらった。ホテルはいつものWestinでなかなかよいホテルである。
さて明日の講演を控えて、拙ブログの記事を見るとたくさんのコメントが入っていて、その反響の大きさに驚いた。
発表用のPowerpointを調整していたところなので、コメントからいくつかのアイデアを戴いた。
歯車を使う工夫をお知らせ戴いた方が多いが、それは試作済みで、すでに不合格の烙印を押されている。細かい歯車を使っても、バックラッシをゼロにはできない。軽く動くようにするには隙間が必要で、そうするとガタが生じ、そのガタは必要な変位量を上回ることがある。それほど捻りの変位量は少ないのである。
リンクの結節点は少なく、ガタの総量を極力極力少なくすることができる。このガタが小さいということが全てで、他のいかなる方法もリンクには敵わない。伊藤剛氏のフカひれ型が優れているのは、結節点が少ないことである。だからガタがほとんどない。ガタがあれば正しく作動しないのである。
それともう一つ、変位量の大きさが完全に2台車間で等しいことが必要である。これもパンタグラフ方式には敵わない。単純なリンク方式では、動きが大きくなると、回転角がまったく等しいとは言えなくなる。これはロンビックも同様である。形が大げさなので難しそうに見えるが、作るのはとても簡単である。滑り込みのパイプさえあればすぐできる。しかも調整がほとんど要らない。リンクの結節点を厚く作って倒れないようにすれば、摩擦はいつも小さく保てる。またバランスが取れているので、作動に力が要らない。
機構学に詳しい方は、きっとこの方式の利点に気が付かれるだろう。先回の改良フカひれ方式では、完全な等角ではないのだ。
ゆうえん氏の記事にあるように、等角逆捻りが目的であって、ロンビックイコライザはその一つの方式に過ぎない。それではどの方法がベストかと言うといまのところ、目的的には、このパンタグラフ方式が最上の方式のようだ。模型であって、ある程度の誤差を含めてもよいなら、フカヒレでもよいし、ロンビックでもよい。
作る模型のサイズの問題もあるし、どのような線路を走らせたいのかにも依るので、解は一つではない。
ちなみに、実物の電車等のパンタグラフには、イコライザと称するリンクが付いている。それが1本の場合とたすき掛け2本の場合がある。前者は動きが滑らかであるが、2本のアームの動きが完全に対称ではない。後者は動きが正確であるはずなのであるが、動きが渋い。作図してみると、どちらもおかしなことに気がつく。リンク機構は大きな稼動範囲をもたせると、具合が悪くなるという実例である。この話は栗生弘太郎氏から伺った話を元にしている。
しばらく休載の予定であったが、所感をまとめてお知らせした。
さて明日の講演を控えて、拙ブログの記事を見るとたくさんのコメントが入っていて、その反響の大きさに驚いた。
発表用のPowerpointを調整していたところなので、コメントからいくつかのアイデアを戴いた。
歯車を使う工夫をお知らせ戴いた方が多いが、それは試作済みで、すでに不合格の烙印を押されている。細かい歯車を使っても、バックラッシをゼロにはできない。軽く動くようにするには隙間が必要で、そうするとガタが生じ、そのガタは必要な変位量を上回ることがある。それほど捻りの変位量は少ないのである。
リンクの結節点は少なく、ガタの総量を極力極力少なくすることができる。このガタが小さいということが全てで、他のいかなる方法もリンクには敵わない。伊藤剛氏のフカひれ型が優れているのは、結節点が少ないことである。だからガタがほとんどない。ガタがあれば正しく作動しないのである。
それともう一つ、変位量の大きさが完全に2台車間で等しいことが必要である。これもパンタグラフ方式には敵わない。単純なリンク方式では、動きが大きくなると、回転角がまったく等しいとは言えなくなる。これはロンビックも同様である。形が大げさなので難しそうに見えるが、作るのはとても簡単である。滑り込みのパイプさえあればすぐできる。しかも調整がほとんど要らない。リンクの結節点を厚く作って倒れないようにすれば、摩擦はいつも小さく保てる。またバランスが取れているので、作動に力が要らない。
機構学に詳しい方は、きっとこの方式の利点に気が付かれるだろう。先回の改良フカひれ方式では、完全な等角ではないのだ。
ゆうえん氏の記事にあるように、等角逆捻りが目的であって、ロンビックイコライザはその一つの方式に過ぎない。それではどの方法がベストかと言うといまのところ、目的的には、このパンタグラフ方式が最上の方式のようだ。模型であって、ある程度の誤差を含めてもよいなら、フカヒレでもよいし、ロンビックでもよい。
作る模型のサイズの問題もあるし、どのような線路を走らせたいのかにも依るので、解は一つではない。
ちなみに、実物の電車等のパンタグラフには、イコライザと称するリンクが付いている。それが1本の場合とたすき掛け2本の場合がある。前者は動きが滑らかであるが、2本のアームの動きが完全に対称ではない。後者は動きが正確であるはずなのであるが、動きが渋い。作図してみると、どちらもおかしなことに気がつく。リンク機構は大きな稼動範囲をもたせると、具合が悪くなるという実例である。この話は栗生弘太郎氏から伺った話を元にしている。
しばらく休載の予定であったが、所感をまとめてお知らせした。
2013年02月12日
続々々 ロンビック・イコライザの幾何学
 「考案者は日本人で、Mr.Dewaである。」と言うと「なんだお前じゃないのか。」と言われた。Patent も出願されていると言ったら、
「考案者は日本人で、Mr.Dewaである。」と言うと「なんだお前じゃないのか。」と言われた。Patent も出願されていると言ったら、「そりゃそうだろうが、このアイデアが売れるかどうかは何とも言えない。」と懐疑的である。
「必ず4支点を同一平面に置いて、ガタが無いようにせねばならない。」と言うと、
「工作がむずかしい。」という評価であった。
「片持ちはお前の発明だろう?」と聞かれたので、
「これもMr.Dewaによる。」と言うと不思議そうだ。
「こちらを特許出願すべきだった。」と言う。
同じ効果なら、より簡単な片持ち式が良いという意見が大半だった。
 等角逆捻りの機能さえあればよいのだから、他にもアイデアがある。と伊藤剛氏のアイデアを、今野氏が16番で作られたものの写真を見せた。これには、会場がどよめいた。
等角逆捻りの機能さえあればよいのだから、他にもアイデアがある。と伊藤剛氏のアイデアを、今野氏が16番で作られたものの写真を見せた。これには、会場がどよめいた。「Dr.Konnoは本当に医者か?模型屋じゃないのか。」という質問に、
「どちらとも決めかねる人です。」と答えると、爆笑した。
 そして、最終的に筆者の作ったコンシールドタイプである。最初は皆、
そして、最終的に筆者の作ったコンシールドタイプである。最初は皆、「これはいったい何?」という顔をしていた。
作動させると、「これは面白い」ということになった。みんなで順に触って、動作を確かめる。
不思議そうな顔をしているが、理屈が分かった途端に晴れ晴れとした顔になるのが見ていて楽しい。
二本のロッドの先端の噛み合いはボールとソケットになっているのが分かると、
「凄いアイデアだ。日本には天才がたくさん居る!」
と叫んだ。
2013年02月08日
続 ロンビック・イコライザの幾何学
 今野氏の作られたロンビック・イコライザの作例をお借りして持って行ったので、出席者はそれを手で触って実感した。この作例は昨年のJAMでのデモ用に製作されたものである。それを少々手直しさせて戴いて、持って行った。
今野氏の作られたロンビック・イコライザの作例をお借りして持って行ったので、出席者はそれを手で触って実感した。この作例は昨年のJAMでのデモ用に製作されたものである。それを少々手直しさせて戴いて、持って行った。
 それ以外に、栗生氏の説明の中にもある台車のボルスタに支えを付けたものも持って行った。これが意外と評判が良く、「面白い!」ということだった。片持ちだと三角型にしかならないと思われるかもしれないが、その三角形は菱形の半分であり、左側は無いように見えても、実は存在している。その三角形は右の三角形と同一平面にあることは自明であろう。3点支持が二つ(見方によっては四つ)在って、それらが同一の平面上にある、すなわち4点支持になるというところがこの工夫の妙である。
それ以外に、栗生氏の説明の中にもある台車のボルスタに支えを付けたものも持って行った。これが意外と評判が良く、「面白い!」ということだった。片持ちだと三角型にしかならないと思われるかもしれないが、その三角形は菱形の半分であり、左側は無いように見えても、実は存在している。その三角形は右の三角形と同一平面にあることは自明であろう。3点支持が二つ(見方によっては四つ)在って、それらが同一の平面上にある、すなわち4点支持になるというところがこの工夫の妙である。
 もちろん片持ちの方には裏からも支えが必要である。これが無いとひっくり返ってしまう。
もちろん片持ちの方には裏からも支えが必要である。これが無いとひっくり返ってしまう。これら二つの作例をご覧戴きたい。この二つは等価である。台車枠そのものをイコライザとして使っているか、台車枠の中にイコライザを仕掛けただけなのか、の違いである。
2013年02月06日
ロンビック・イコライザの幾何学
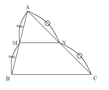 栗生氏の証明に沿って説明しよう。中学校の幾何の時間に、中点連結定理というのがあった。三角形の二辺の中点を結ぶと底辺に平行になるというものだ。これは簡潔明瞭な定理であって、証明は容易である。
栗生氏の証明に沿って説明しよう。中学校の幾何の時間に、中点連結定理というのがあった。三角形の二辺の中点を結ぶと底辺に平行になるというものだ。これは簡潔明瞭な定理であって、証明は容易である。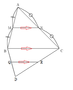 今度はその三角形の底辺同士を重ねて任意の四角形を作って見る。すると中点を結んだ線分同士が平行になる。要するに任意の四角形の各辺の中点を結ぶと、必ず平行四辺形が生まれるというわけだ。見方を変えれば、四角形の対角線と、それによって二分されて生じる三角形の中点連結線分は平行になるということである。もう一つの対角線についても全く同様であるから、必然的に平行四辺形が生まれることになる。
今度はその三角形の底辺同士を重ねて任意の四角形を作って見る。すると中点を結んだ線分同士が平行になる。要するに任意の四角形の各辺の中点を結ぶと、必ず平行四辺形が生まれるというわけだ。見方を変えれば、四角形の対角線と、それによって二分されて生じる三角形の中点連結線分は平行になるということである。もう一つの対角線についても全く同様であるから、必然的に平行四辺形が生まれることになる。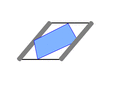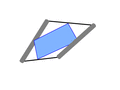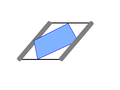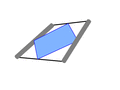 ロンビック・イコライザの幾何学はこれで終了である。実に簡単な証明であって、明快である。大切なことはこれらの4支点が同一平面上に来ることだ。いくつか作例を見せて戴いたが、支点があらぬところにあって驚くことがある。それでは完全な平面上に置いたときは問題ないが、変位があると、あちこちで矛盾が生じるだろう。動きが渋いのは、たいていそういう種類の間違いから生じている。
ロンビック・イコライザの幾何学はこれで終了である。実に簡単な証明であって、明快である。大切なことはこれらの4支点が同一平面上に来ることだ。いくつか作例を見せて戴いたが、支点があらぬところにあって驚くことがある。それでは完全な平面上に置いたときは問題ないが、変位があると、あちこちで矛盾が生じるだろう。動きが渋いのは、たいていそういう種類の間違いから生じている。 当初は原理が証明されていなかったので、この種の間違いに気が付かなかったのは仕方が無い。しかし今後作る時には、この点を十分に考慮した設計をするべきである。
当初は原理が証明されていなかったので、この種の間違いに気が付かなかったのは仕方が無い。しかし今後作る時には、この点を十分に考慮した設計をするべきである。2013年02月04日
Clinic
 O Scale West 2013 は、1月25,26日に Santa Clara で開かれた。サンタクララはサンホゼの隣の市である。
O Scale West 2013 は、1月25,26日に Santa Clara で開かれた。サンタクララはサンホゼの隣の市である。年末に講演会の打診があったので請けた。意外に皆さんが期待してくれている。「何か面白い話をするだろうと毎年楽しみにしている」と、言われた。
今回の講演は例のロンビック・イコライザの話だ。英語であるから、表現は多少改めた。菱型は Rhomboid であるから、その形容詞形は Rhomboidal になる。幾何学用語をおさらいして、間違いのない表現を心掛けた。出席者は約20人であったが、全員技術畑の人ばかりで、隙があったら突っ込まれる、やや緊張感のある講演会であった。
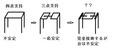
 「3点支持が不整路面に対応する唯一の方法である」ということは、長年にわたる常識であった。ロンビック・イコライザはそれを覆した。良く考えてみれば、4本の足を二組に分けて、台の部分に対し回転するようにしてその回転角が正反対に均等になるようにすればよいことである。要するに制御された二点支持である。(この考え方は栗生氏の記事の追記4に紹介されている。2013年2月9日追記)
「3点支持が不整路面に対応する唯一の方法である」ということは、長年にわたる常識であった。ロンビック・イコライザはそれを覆した。良く考えてみれば、4本の足を二組に分けて、台の部分に対し回転するようにしてその回転角が正反対に均等になるようにすればよいことである。要するに制御された二点支持である。(この考え方は栗生氏の記事の追記4に紹介されている。2013年2月9日追記)この捻(ひね)りを掛ける方法はいくつかある。仰々しく考えれば、センサとサーボ・モータで動かすことができる。それを幾何学的に行うことができれば自然にできるはずだ。
ロンビック・イコライザの理論的解明は長年の懸案事項であったが、2009年に栗生弘太郎氏が証明されたので、非常にクリアになった。今までロンビックだと発表されていたものも、この証明により微妙な間違いが露呈したものもある。4つの支点が完全に同一平面になければならないのである。すなわち、作用点(力点)を含め、8点が同一平面になければならない。